Geometric Transformation
목차
기초 수학
● Point, Scalars and Vectors
Point : location in space. 공간에 한 지점
Scalar : real number, e.g distance. 방향성이 없는 크기
Vector : direction with magnitude. 방향성이 있는 크기

● Line
Parametric form of a line (선의 매개변수 방정식) : $$ P(a) = P_{0} + \alpha d $$
P0 = origin 시작점
a : 임의의 스칼라값
d : 임의의 방향 벡터
Cartesian Coordinate(데카르트 좌표게, 직교 좌표계)에서는 2D 벡터를 2개의 평행하지 않은 벡터의 조합으로 표현할 수 있습니다.
$$ a = \begin{bmatrix}
x_{a} \\
y_{a}
\end{bmatrix} $$
● 내적 ( Dot product, scalar product, inner product )
$$ a\cdot b = \left\| a\right\|\left\| b\right\|cos\Theta $$
벡터 a, b를 가지고 내적을 한다는 것은 벡터 a를 벡터 b에 대하여 정사영 하는 것입니다.
내적을 하면 결과가 스칼라 값이 나오기에 스칼라 곱이라고도 합니다.
벡터 a, b를 직교 좌표계에서 표현하면
$$ a = (x_{a}, y_{a}), b = (x_{b}, y_{b}), then a\cdot b = x_{a}x_{b} + y_{a}y_{b} $$
로 나타낼 수 있습니다.
이는 다양한 방식으로 사용될 수 있는데 대표적인 예로 Player가 있을 때 몬스터의 전방(head), 후방(tail)을 확인하는데 사용될 수 있습니다.

● 외적 ( Cross Product, vector product, outer product )
$$ a \times b = ( y_{a}z_{b} - z_{a}y_{b}, z_{a}x_{b} - x_{a}z_{b}, x_{a}y_{b} - y_{a}x_{b} ) $$
벡터 a, b 를 가지고 외적을 진행하면 벡터 a, b 모두에 대해 수직인 직교 벡터를 구할 수 있습니다.
외적은 x,y,z축 3차원에 대해서 가능하며 2차원에 대해서는 임의의 한 축을 0으로 취급하여 사용할 수도 있습니다.
일반적으로 3차원 공간에서 좌표를 잡는 오른손 법칙을 기준으로 a에서 b 벡터 방향으로 손을 움켜쥘 때 엄지의 방향이 새로운 직교 벡터에 방향이 됩니다.

외적을 계산할 때는 다음과 같이 암기하기 좋은데, 새로운 직교 벡터의 x축 성분을 얻기 위해서는 기존 벡터 a, b에 x축 성분을 사용하면 안된다고 생각하면 편한 것 같습니다.
외적의 크기는 다음과 같습니다.
$$ \left\| a\times b \right\| = \left\| a\right\| \left\| b\right\| sin\Theta $$
이는 벡터 a, b로 만들어지는 평행사변행의 넓이와 같아 a, b 로만들어지는 삼각형의 넓이를 구하는데 쓰입니다.

● 좌표계
좌표는 다양한 좌표계로 표현될 수 있으며 각 물체에 좌표는 Global/World에서의 좌표와 물체 자신의 Object 좌표 등등으로 나뉠 수 있습니다.
예를들어 월드 좌표는 직교 좌표이지만 해당 기능이 물체를 중심으로 회전하는 경우 원형, 원통 좌표계를 사용할 수 있습니다.
2D Geometric Transformation
● Linear Transformation (선형 변환, Linear mapping, Linear function)
사전적으로는 두 벡터 공간 V, W가 있을 때 V → W에 대한 변환 함수 T가 다음 조건들이 서로 동치면 선형변환이라고 합니다.
f (u + v) = f(u) + f(v)
f(cu) = cf(u)
선형 변환은 덧셈 연산과 스칼라를 곱하는 것이 보존되며, 항상 선형 부분공간에서 선형 부분공간으로 매핑합니다.
아래는 그래픽스에서 쓰는 선형 변환들입니다.
● 기타 선형 변환
크기(Scale), 회전(Rotation), 전단(Shear), 반전(Reflection)이 있지만 모든 2D 기하 변환은 3D에도 적용 가능하기에 skip..
3D Geometric Transformation
● 아핀 변환(Affine Transformation)과 Homogeneous Coordinate (동차좌표)
아핀 변환은 선형변환(Linear Transformation) + 이동변환(Translation) 결합으로 점, 직선, 평면을 보존하는 두 아핀 공간 사이의 선형 매핑입니다.
동차좌표란 n차원 사영 공간을 n+1개의 좌표로 나타내는 좌표계라고 한다...
간단히 생각해서 행렬에 차원을 추가하고 그 이유는 선형변환과 평행이동(Translation), 즉 아핀 변환을 동시에 표현할 수 있습니다.
$$ \begin{bmatrix}
x_{a} & y_{a} & z_{a} & 0 \\
x_{b} & y_{b}& z_{b} & 0 \\
x_{c} &y_{c} & z_{c} & 0 \\
0& 0 &0 &1 \\
\end{bmatrix} $$
위와 같이 3x3 행렬로 3차원 표현을 4x4로 바꿔 이동 변환과 현재 행렬이 점인지 벡터인지 판정할 수 있습니다. 1이면 점, 0이면 벡터입니다.
● 3D 평행이동 (Translation)

(x, y, z)좌표 P에 3D 평행이동 T를 곱해 P'으로 평행이동합니다.
● 3D 크기 변환 (Scaling)

(x, y, z)좌표 P에 크기 S로 Scale을 곱해서 위치 변경합니다.
● 3D 회전 변환 (Rotation)
3D회전변환은 회전 축이 나를 바라보는 방향으로 반시계 방향으로 Θ 각도만큼 회전이 현재 표준으로 잡혔습니다.
● 회전행렬
$$ \begin{matrix}
x' = \rho cos(\theta + \phi ) = cos \theta x - sin \theta y \\
y' = \rho sin(\theta + \phi ) = sin \theta x + cos \theta y \\
\end{matrix} $$
2차원에서의 회전 행렬은 삼각함수의 합차 공식을 이용하면 xy평면에 대한 좌표점의 회전을 쉽게 공식화할 수 있다고 합니다.

해당 회전을 행렬로 다음과 같이 표현합니다.
3D 회전변환도 위 행렬을 바탕으로 하는데 x, y, z축을 중심으로 회전하여 총 3번의 회전으로 표현할 수 있습니다.

여기서 왜 y축 중심 회전만 sinθ 부호가 반대인가? 생각할 수 있습니다. 해당 부분을 이해하기에 정말 많이 찾아봤고... 아직도 조금 애매하지만 이유는 다음과 같습니다.

위에서 3D 회전 변환은 "회전 축이 나를 바라보는 방향으로 반시계 방향으로 θ 각도만큼 회전하는 것을 표준으로 잡혔다"라고 했는데 여기서 3차원 직교 좌표계를 생각했을 때 x에서 회전 시 xy평면이, z에서 회전시 yz평면이 회전합니다. 하지만 y에서 회전시 zx평면이 회전하는 것을 볼 수 있습니다. xz평면에 반대로 회전하기에 zx평면 기준 회전으로는 y축 반시계 회전은 자연스러운 형태였습니다.

이를 좀 더 직관적으로 보자면 3x3회전행렬을 확장시켜 6x6행렬로 표현하면 우측부터 z, y, x 회전으로, 행렬의 순환순서를 추적할 때 세 행렬이 동일한 것을 볼 수 있습니다.
*엄숙한? 회전
DirectX12를 이용한 3D 게임 프로그래밍 입문 - 회전
벡터 V를 축 n을 중심축으로 회전한다고 할 때 V를 두 부분으로 분해 가능합니다.
1. n에 평행한 성분 : proj(V)
2. n에 직교인 성분 perp(V) = V - proj(V). *perpendicular : 수직선
여기서 proj(V)는 n에 평행하니 회전에 대해 불변(invariant)합니다.
V가 회전된 벡터를 R(V)라고 할 때, R(V)는 proj(V) + R(V┹)입니다.
여기서 V┹는 n에 직교성분으로 V - proj(V)입니다.
또한 n과 V를 외적한 것에 크기가 V┹크기와 같다는 것은 그림을 통해 알 수 있습니다.
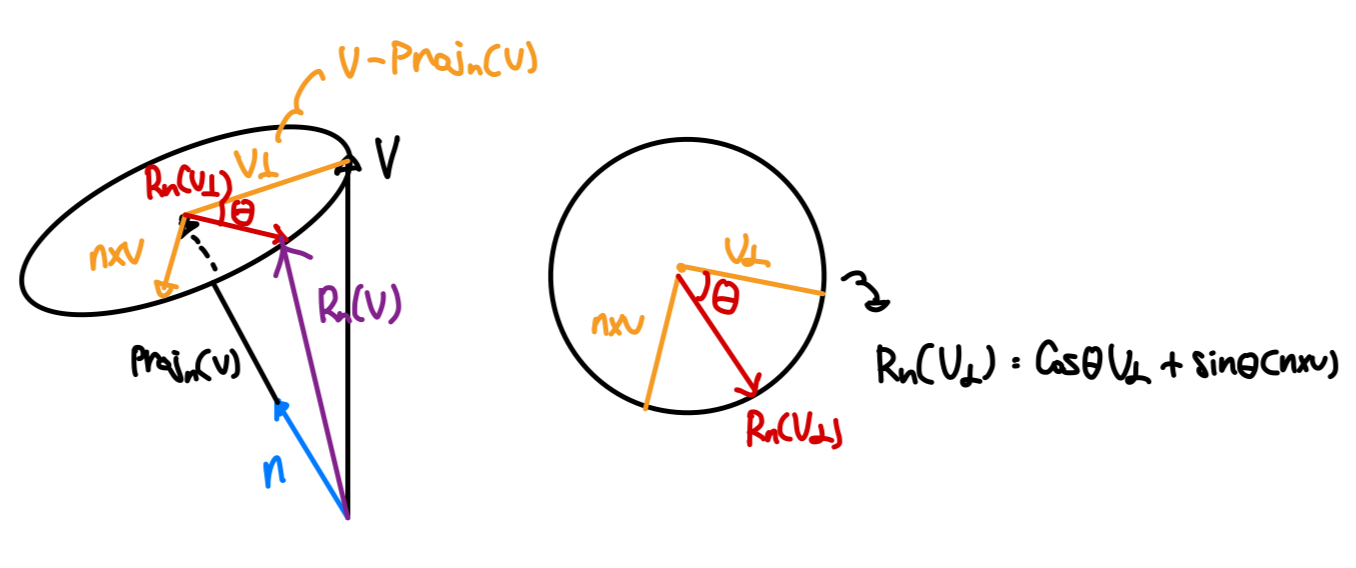
위 식에서 R(V┹) = cosθ V┹ + sinθ (nxV)로 회전공식을 도출할 수 있고, 이 회전공식을 표준기저벡터에 적용해 행렬로 표현하면 다음과 같은 회전 행렬을 구할 수 있습니다.
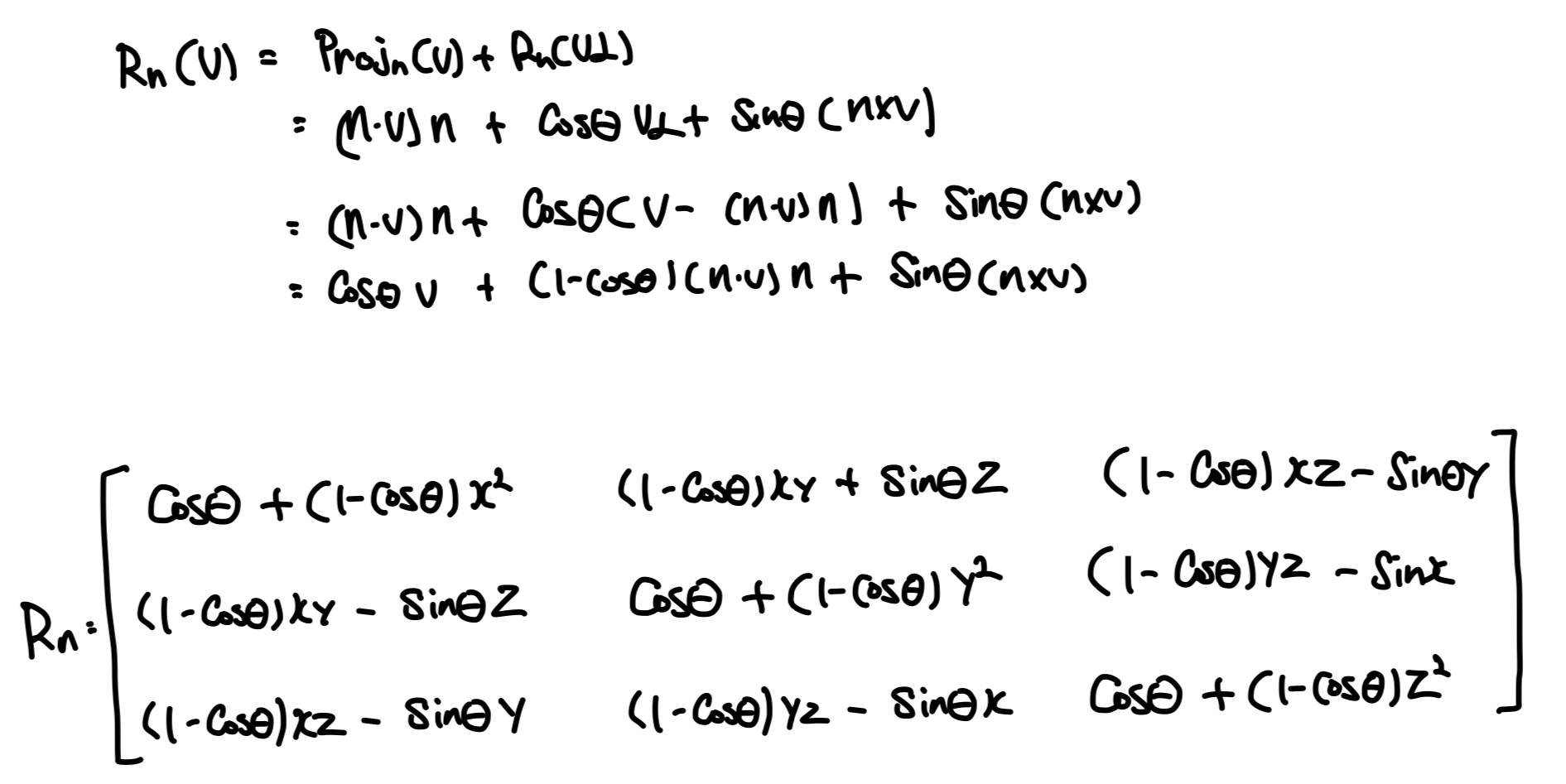
특징으로 각 행벡터가 단위길이이며 서로 직교이기 때문에 행벡터들이 정규직교를 이루고, 직교행렬은 그 역행렬이 전치행렬이니, 전치행렬이 역행렬이 됩니다.
마지막으로 회전축의 좌표를 각각 x(1,0,0), y(0,1,0), z(0,0,1), 즉 표준기저벡터를 대입하면 위 회전행렬과 동일한 값이 도출됩니다.
■ 일반적인 3D 회전 변환
회전 변환은 일반적으로 다음 과정을 거칩니다.
1. 회전 시킬 것을 원점으로 평행이동 합니다. (T)
2. 회전할 축이 없는 평면에 내립니다. y축을 중심으로 회전한다면 x, z축 중심으로 회전해 xz평면에 내립니다. (Rx, Rz)
3.y축 기준 회전을 합니다. (Ry)
4. 이전 2, 1과정을 역행렬로 복귀시킵니다.

이렇게 축을 중심으로 회전을 x, y, z에 대해 할 수 있습니다. 이를 좀 더 간단히 하기 위해 원점으로 평행이동 과정과 특정 평면에 내리는 과정을 XYZ 좌표계에서 이것이 완료된 UVW 직교 좌표계로 변환시키는 방법이 가능합니다.

● 법선 벡터와 평면의 방정식
법선 벡터 n = (a, b, c)이고 법선과 평면이 맞닿는 한 점이 (x0, y0, z0)일 때 평면의 방정식은 다음과 같습니다.

평면 위 벡터는 임의의 기하 변환 후에도 보전되지만, 평면의 법선 벡터는 임의의 기하 변환 M 후에는 법선이 아닙니다.
이때 임의의 기하 변환 M이 적용될 때 법선 벡터에 적용되는 변환 N은 (M^-1)^T 즉 M의 역행렬에 전치행렬입니다.