Surfaces
목차
- Surface
- Surface Method used in geometric modeling
- Curves to Surfaces(Bezier Surface)
- Bezier Surface Derivatives
Surfaces
Parameterized Surface
연속 곡면(Surface) s ⊂ R³ 는 다음과 같은 매개화(parameterized)된 형태로 표현할 수 있습니다.
$$ X(u, v) = \begin{pmatrix}
x(u, v) \\
y(u, v) \\
z(u, v)
\end{pmatrix},(u,v)\in \Omega \subset R^{2} $$
x(u,v), y(u,v), z(u,v)는 미분 가능한 함수
Ω는 매개 변수의 정의역(parametric domain)
u, v는 매개변수의 좌표(coordinate)
u, v상 좌표를 x로 매핑해 곡면을 만듭니다.

- 구면 (Sphere Surface)

● 곡면의 특성
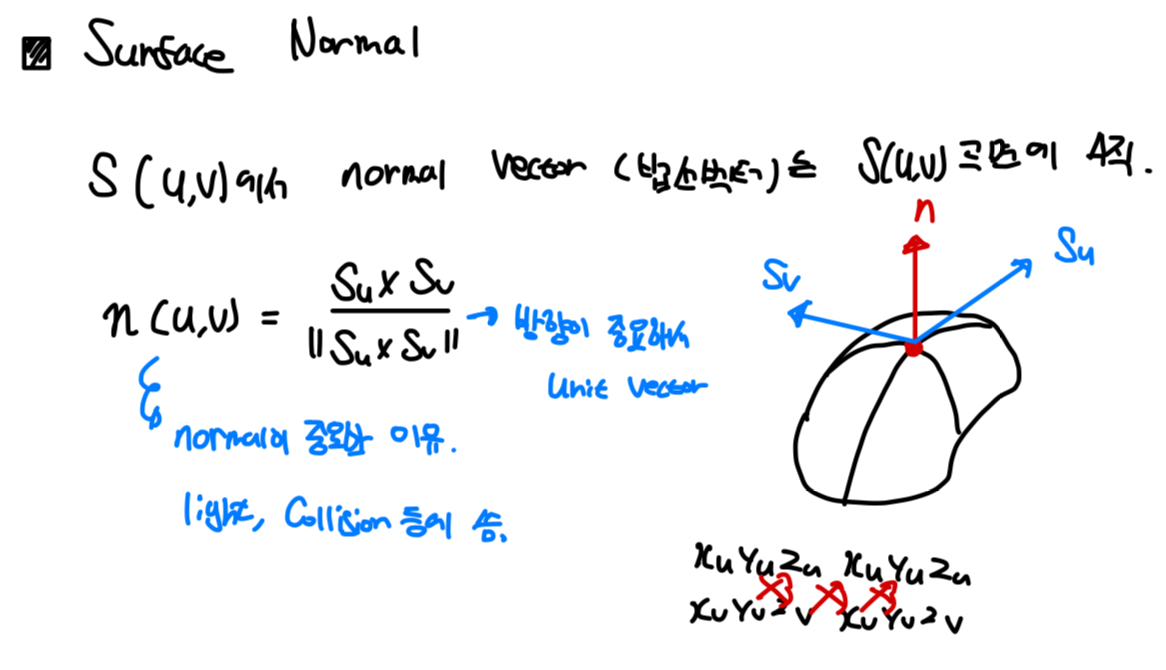
곡면의 한 점 X(u, v)에서 순간적인 v방향 기울기 ∂X / ∂ , u방향 기울기 ∂X / ∂u를 구하고 이 두개를 외적해서 나오는 새로운 벡터가 Surface에 순간적인 빛 반사 등 여러 곳에 많이 쓰인다고 합니다.

Surface method used in Geometric modeling
Bilinear Patch
b₀₀, b₀₁, b₁₀, b₁₁ 의 네 점으로 b₀₀, b₀₁을 선형 보간(p₀₀), b₁₀, b₁₁을 선형 보간(p₀₁) , 그렇게 만들어지는 p₀₀, p₀₁ 사이점을 선형보간 하면 생기는 곡면입니다.
X(u,v) = (1-u)(1-v) b₀₀ + (1-u) v b₀₁ + u(1-v) b₁₀ + uv b₁₁ { (u,v) : 0 ≤ u, v ≤ 1 }
$$ => X(u,v) = [1-u]\begin{bmatrix}
b_{00} &b_{01} \\
b_{10} &b_{11} \\
\end{bmatrix}\begin{bmatrix}
1-v \\
v
\end{bmatrix} $$

Ruled Surface
두 곡선 a(t)와 b(t)가 있을 때 다음의 곡면을 생성합니다.
X(u,v) = v a(u) + (1-v) b(u)

a(u)와 b(u)가 만드는 곡선이 b₀₀, b₀₁, b₁₀, b₁₁ 네 점이 만드는 곡선과 같고 선형보간 되면 Bilinear Patch와 동일합니다.
Surface of Revolution (회전)
한 단면을 그리고 특정 지정 축으로 회전시켜 생성합니다. 모델링 툴에서도 자주 보이는 기능입니다.
B(t) = (Bx(t), 0, Bz(t)) 형태의 커브가 있고 Z축을 기준으로 회전시키면
x(u, v) = Bx(u)cos(v)
y(u, v) = Bx(u)sin(v)
z(u,v) = Bz(u)
수식이 됩니다.

Extrusion Surface
Extrusion(밀어내다, 분출, 돌출) 방식으로 평면 곡선을 선형적인 방향으로 돌출시킵니다.
평면 곡서늘 B(t), 돌출 방향을 V라 할때 X(u, v) = B(u) + vV 곡면을 생성합니다.

Curves to Surfaces
곡선(Curve)은 제어점과 basis function들의 내적으로 표현됩니다.(함수 + 제어점)
곡면(Surface)은 Curve 들의 Curve로 표현할 수 있습니다. 이렇게 만든 Surface는 tensor product surface라고 정의합니다.
Bezier Surface
● Bezier Curve 표현

● Bezier Surface 표현

● Bilinear Pacth와 관계
Bilinear Patch는 가장 간단한 Bezier Surface이기도 합니다. 1X1 Bezier Surface

● m차 x n차 Bezier patch 표현
$$ S(u, v) = [B_{0}^{m}(u) \cdots B_{m}^{m}(u)]\begin{bmatrix}
P_{0,0} &\cdots &P_{0,n} \\
\vdots & &\vdots \\
P_{m,0} &\cdots &P_{m,n} \\
\end{bmatrix}
\begin{bmatrix}
B_{0}^{n}(v) \\
\vdots \\
B_{n}^{n}(v)\\
\end{bmatrix} $$

* 문제예시

● Bezier Patch 특성

Bezier Surface Derivatives
곡면의 미분(derivative) : 곡면 상의 한 점을 지나는 두 isocurve들의 접선
u - partial derivative at S(u₀,v₀) : S(u, v₀)의 접선 = Su(u,v) = ∂S(u,v) / ∂u
v - partial derivative at S(u₀,v₀) : S(u₀, v)의 접선 = Sv(u,v) = ∂S(u,v) / ∂v
위 문제 예시에서 Sv(0.5, 0.5)는?
● Surface Normal